2014년에는 ILSVRC 대회에서 GoogleNet 이 1등(6.7% 에러율) VGGNet이 2등(7.3% 에러율)을 차지하였다면 2015년에는 ResNet이 3.57%의 에러율을 가지며 전년도 1~2등의 에러율의 거의 절반에 가까운 성능을 보이면서 압도적으로 1등을 하였다.
ResNet은 그 유명한 'Kaiming He'님이 설계를 하였고 당시 마이크로소프트 북경연구소, 현재는 FAIR(Facebook AI Research에 소속되어 계신다. ResNet의 가장 큰 특징이라고 하면 깊은 망(레이어)와 residual learning인데 논문 내용을 통해 ResNet에 대해 자세히 알아보자.
깊은 망의 문제점
CNN에서 파라미터를 업데이트 할때 gradient 값이 너무 크거나 작아지게 되면 더이상 학습이 진행되지 않게되는 문제가 있다. 그래서 이 문제를 해결하기위해 Batch Normalization, 파라미터 초기값 개선 등 여러 기법들이 적용되고 있지만 여전히 layer 개수가 일정 수를 넘어가게 되면 여전히 골치 거리가 된다.
training과정에서 이론적으로는 망이 깊어지면 깊어질수록 성능이 좋아져야 한다. 하지만 실제로 레이어를 무작정 많이 쌓게되면 파라미터는 비례적으로 늘어나게 되고 overfitting의 문제가 아닐지라도 오히려 에러가 커지는 상황이 발생한다.
ResNet 팀은 망이 깊어지는 경우 어떤 결과가 나오는지 보여주기 위해 작은 실험을 하게 된다. 비교적 간단한 데이터셋인 CIFAR-10으로 20-layer와 56-layer에 대하여 비교실험을 하였고 결과는 아래와 같다.
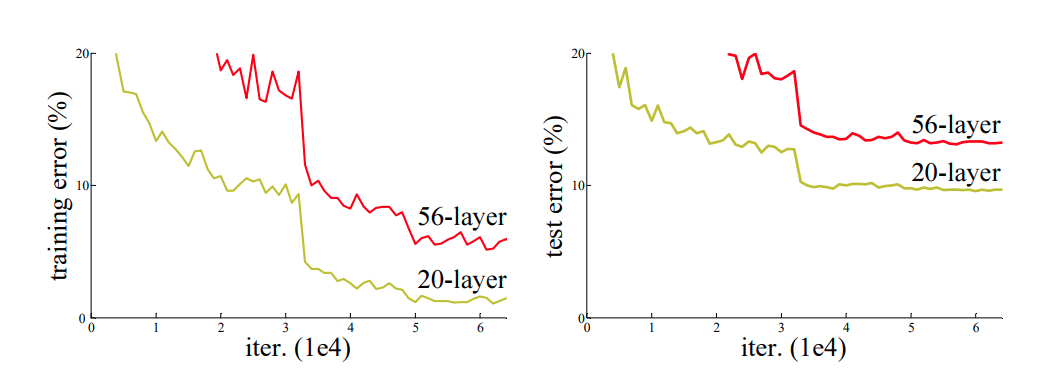
일반적인 CNN기법을 사용을 하면 training 과 test 시에 둘다 레이어가 깊어질수록 성능이 나빠진다는 것을 보여주었다. 이러한 문제를 해결하기위해 deep residual learning의 개념이 나오게 된다.
Residual Learning
먼저 아래와 같이 평범한 CNN 망을 살펴보자. 이 망은 입력 x를 받아 2개의 weighted layer(convolution layer)를 거쳐 출력 H(x)를 내며, 학습을 통해 최적의 H(x)를 찾는 것이 목표이며, weighted layer의 파라미터 값은 최적의 H(x)를 만들기 위한 값으로 결정이 되어야 한다.
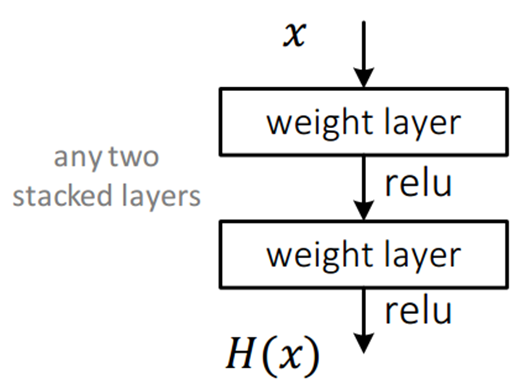
그런데 여기서 H(x)를 얻는 것이 목표가 아니라 H(x) - x를 얻는 것으로 목표를 수정한다면, 즉 출력과 입력의 차를 얻을 수 있도록 학습을 하게 된다면, 2개의 weighted layer는 H(x) - x를 얻도록 학습이 되어야 한다. 여기서 F(x) = H(x) - x 라면, 결과적으로 출력 H(x) = F(x) + x가 된다.
그러므로 위 그림은 아래 그림처럼 바뀌게 되며, 이것이 바로 Residual Learning의 기본 블락이 된다. 위와 달라진 점은 입력에서 바로 출력으로 연결되는 Idenrtity shortcut이 생기게 되었고 이 shortcut은 파라미터 없이 단순히 덧셈만 수행되기 때문에 연산량 관점에서는 별 차이가 없다.(논문에서는 두개의 conv마다 shotcut연결을 하였음)
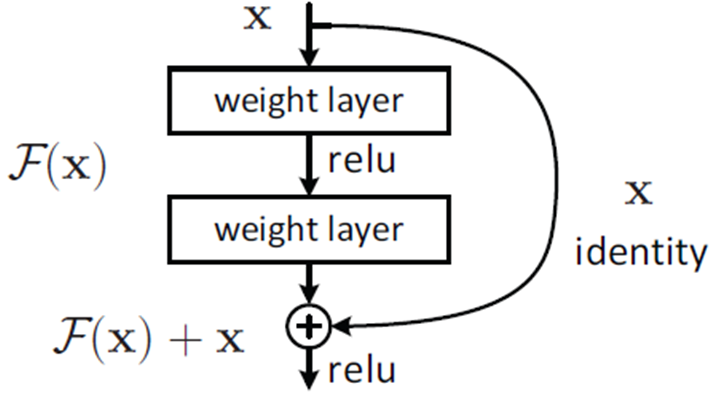
관점을 조금만 바꾼 것 뿐이지만 꽤 많은 효과를 얻을 수 있게 된다. 가중치를 전부 계산해야 하는 H(x)를 학습하는 것이 아니라 F(x) + x 에서 x는 이미 알고 있는 것이고 결국 F(x)에 대해서만 학습을 진행하게 되는 것이기 때문에 망이 깊어지더라도 그 정보가 계속 유지될 수 있으며 학습도 잘 된다.
Identity shortcut 연결을 통해 얻을 수 있는 효과는 다음과 같다.
- 깊은 망도 쉽게 최적화 가능하다.
- 늘어난 깊이로 인해 정확도를 개선할 수 있다.
ResNet은 classification에서 152 layer를 사용하여 top-5 에러율이 3.57 %가 나오게 되면서 사람의 오차율인 5% 정도 보다도 더 좋은 결과를 얻었으며, 아래 그림과 같다.
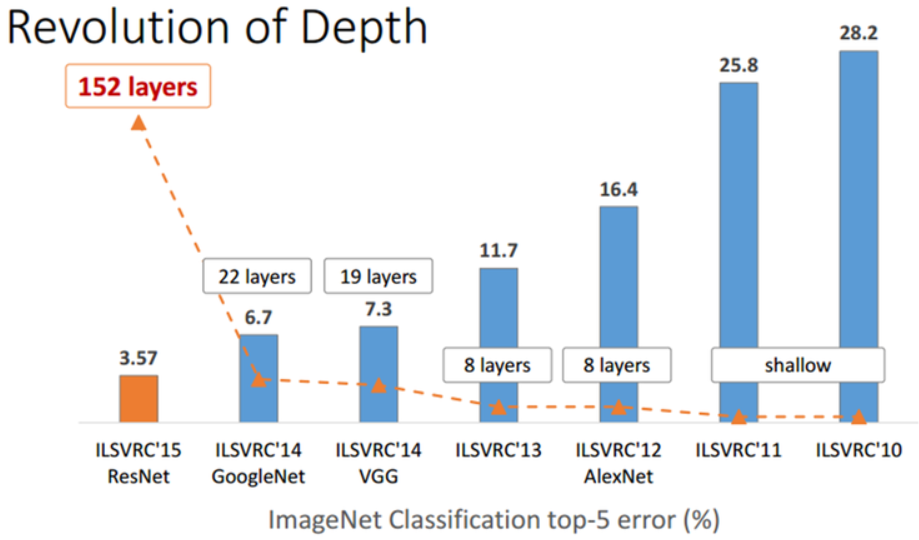
ResNet 팀의 실험
ResNet팀은 VGGNet의 설계 철학을 많이 인용하여 대부분의 layer에서 3x3 kernel 을 사용하고 연산량을 줄이기 위해 max pooling과 FC layer, dropout을 사용하지 않았다.
1. 출력 feature-map 크기가 같은 경우, 해당 모든 layer는 모두 동일한 수의 filter를 갖는다.
2. 연산량의 균형을 맞추기 위해 Feature-map 사이즈가 절반으로 작아지게 되면 filter 수를 두배로 늘린다. (위에서 max pooling으로 feature-map 사이즈를 줄이는 대신 conv 계산에서 필요시에만 stride=2를 사용하여 이미지를 절반으로 줄인다.)
ResNet팀은 일반적인 CNN을 Plain net 이라고 이름을 정했고 이 Plain net과 Resnet을 비교하기 위해 각각 network에 대해 18-layer와, 34-layer 에 대한 실험을을 진행하였고 아래와 같다.
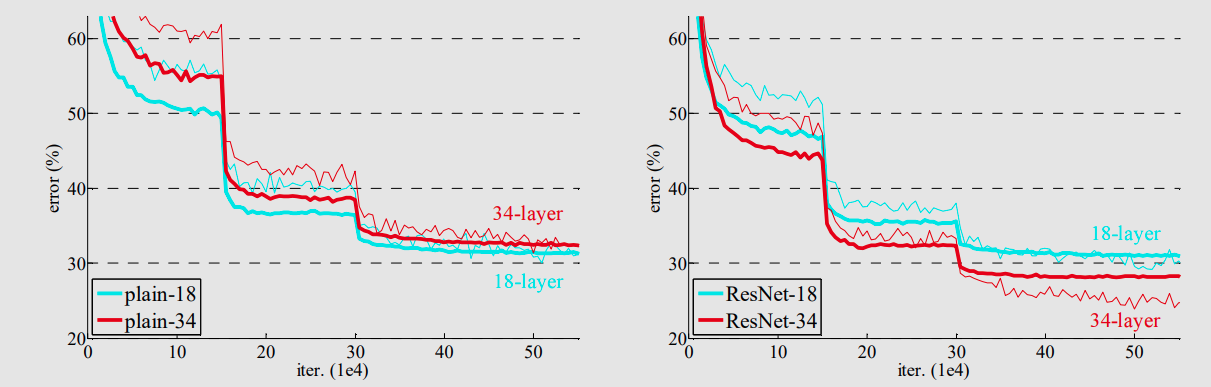
위의 그래프를 보면 알 수 있듯이 일반적인 Plain net은 18-layer 에 비해 34-layer의 성능이 약간 나쁘다는 것을 알 수 있고 반대로 ResNet은 34-layer의 성능이 18-layer보다 좋은 것을 확인 할 수가 있다.
여기서 또 주목해야 할 점은 초기 수렴속도가 ResNet이 더 빠르다는 것도 확인 할 수 있다. 결국 ResNet이 일반적인 Plain network보다 더 빠르고 성능이 좋다는 것이다.
ResNet팀은 50-/101-/152-layer에 대해서는 연산량을 절감하기 위해 GoogleNet의 Inception구조와 같이 1x1 convolution을 이용하여 학습을 진행하였다.
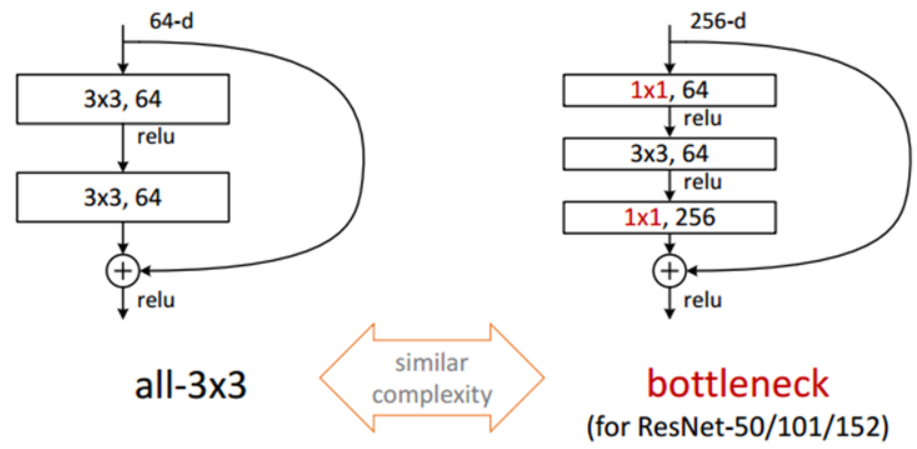
1x1 conv로 dimension을 줄인 뒤에 3x3 conv 연산을 하고 다시 1x1 conv로 dimension을 확대 시켜버리면 그냥 3x3 conv layer 두개를 연결시킨 구조에 비해 연산량을 절감하여 시간을 절약할 수 있다.
지금까지 ResNet의 Residual Learning에 대해 알아보았다. 이제는 코딩을 통해 Resnet을 직접 구현해보자
모델 구현 및 학습
모델 : ResNet18(gpu상황을 고려하여 가장 작은 18-layer를 사용)
데이터 : CIFAR-10 (10개의 클래스 보유, number of train data: 50000, number of test data:10000)

Import Library
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.backends.cudnn as cudnn
import torch.optim as optim
import os
Define Residual Block
class BasicBlock(nn.Module):
def __init__(self, in_planes, planes, stride=1):
super(BasicBlock, self).__init__()
self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=3, stride=stride, padding=1, bias = False)
self.bn1 = nn.BatchNorm2d(planes)
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes)
self.shortcut = nn.Sequential()
if stride !=1:
self.shortcut = nn.Sequential(
nn.Conv2d(in_planes, planes, kernel_size=1, stride = stride, bias=False),
nn.BatchNorm2d(planes)
)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.bn2(self.conv2(out))
out += self.shortcut(x)
out = F.relu(out)
return out - 위의 코드에서 눈여겨 봐야 할 것은 residual block에는 2개의 convolution layer와 shorcut 그리고 activation function이 있다. self.conv1 에서 다음 사이즈 즉 절반으로 feature_map 을 만들때 stride는 2가 되어야 하고 두번째 반복에서는 feature_map 사이즈가 같으므로 stride가 1이 되어야 하기 때문에 stride는 변수로 받게된다.
- 또한 shortcut은 단순히 2번째 convolution layer의 결과값과 더하기만 하지만 이것또한 차원이 맞아야 덧셈이 가능하다. 그러므로 만약 filter가 64 에서 128로 가게 될때 self.conv1 에서 stride는 2가 될 것이고 shortcut도 덧셈을 위해 차원을 같이 따라가야 하므로 1x1 conv를 이용하여 feature_map 사이즈와 filter 사이즈를 똑같이 만들어 준다.(feature_map size, channel 다 같아야지 element wise sum 가능)
- 가장 중요한것은 2번째 conv layer의 결과 값과 shortcut의 값을 더해준 뒤에 activation function(relu)을 사용해야 한다.(forward 함수를 보면 이해할 수 있을 것이다.)
Define ResNet18 Architecture
class Resnet(nn.Module):
def __init__(self, block, num_block, num_classes=10):
super(Resnet, self).__init__()
self.in_planes=64
self.conv1 = nn.Conv2d(3,64,kernel_size=3, stride=1, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(64)
self.layer1 = self._make_layer(block,64, num_block[0], stride=1)
self.layer2 = self._make_layer(block,128, num_block[1], stride=2)
self.layer3 = self._make_layer(block,256, num_block[2], stride=2)
self.layer4 = self._make_layer(block,512, num_block[3], stride=2)
self.linear = nn.Linear(512,num_classes)
def _make_layer(self, block, planes, num_blocks, stride):
strides = [stride] + [1] * (num_blocks - 1)
layers = []
for stride in strides:
layers.append(block(self.in_planes, planes, stride))
self.in_planes = planes
return nn.Sequential(*layers)
def forward(self,x):
x = F.relu(self.bn1(self.conv1(x)))
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x) # 4x4x512
x = F.avg_pool2d(x,4) #1x1x512
x = x.view(x.size(0), -1)
x = self.linear(x)
return x- 위의 코드는 Resnet18의 틀을 정의한 코드이다.
- residual block을 수행하기 전에 논문에서는 7x7 kernel. stride 2를 사용한다고 했는데 CIFAR10 은 이미지가 작기 때문에 3x3 kernel, stride 1을 사용하였다. residual block은 크게 4단계로 filter개수에 따라 혹은 feature_map 사이즈에 따라 나뉜다. 첫번째 레이어(64 filter,32x32 feature_map)에서도 stride 1 을 사용하고 나머지 2,3,4 레이어에서는 첫번째 반복의 첫번째 conv에서 stride 2 를 사용한다.
- 네번째 레이어 까지 수행하면 512 filter 4x4 feature_map 이 되는데 논문에서는 이때 논문에서는 512 filter 7x7 feature_map 이 나오고 여기서 7x7 avg_pooling을 하므로 여기서는 4x4 avg_pooling을 하였다. 그 후 batch_size x 512 x 1 x 1 인 차원을 벡터화 하여 batchsize x 512 로 만들고 linear 연산을 통해 512를 10으로 즉 class 개수로 만들어 준다.
Generate the model
def Resnet18():
return Resnet(BasicBlock,[2,2,2,2])- 여기서 [2,2,2,2]는 각각의 레이어의 residual block의 반복 횟수인데 논문에서도 2번씩 진행하므로 똑같이 하였다.
Data preprocessing
import torchvision
import torchvision.transforms as transforms
transform_train = transforms.Compose([
transforms.RandomCrop(32, padding=4),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010)),
])
# Normalize the test set same as training set without augmentation
transform_test = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010)),
])
train_dataset = torchvision.datasets.CIFAR10(root='./data',train=True, download=True, transform=transform_train)
test_dataset = torchvision.datasets.CIFAR10(root='./data',train=False, download=True, transform=transform_test)
trainloader = torch.utils.data.DataLoader(train_dataset, batch_size=32, shuffle=True, num_workers=4)
testloader = torch.utils.data.DataLoader(test_dataset, batch_size=32, shuffle=False, num_workers=4)- data의 std와 mean값은 데이터 정보를 찾아서 가져왔다. (DataLoader의 batch_size는 32)
Define train method
device = 'cuda' if torch.cuda.is_available() else 'cpu'
net = Resnet18()
net = net.to(device)
cudnn.benchmark=True
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.1, momentum=0.9, weight_decay = 0.0002)
def train(epoch):
print(f'\n[Train epoch: {epoch}]')
net.train()
train_loss = 0
correct = 0
total = 0
for batch_idx, (inputs, targets) in enumerate(trainloader):
inputs, targets = inputs.to(device), targets.to(device)
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outputs, targets)
loss.backward()
optimizer.step()
train_loss += loss.item()
_, predicted = outputs.max(1)
total += targets.size(0)
correct += predicted.eq(targets).sum().item()
if batch_idx % 100 == 99:
print('\nCurrent batch:', str(batch_idx+1))
print('Current benign train accuracy:', str(predicted.eq(targets).sum().item() / targets.size(0)))
print('Current benign train loss:', loss.item())
print('\nTotal benign train accuarcy:', 100. * correct / total)
print('Total benign train loss:', train_loss)- 모델을 cuda로 바꾸었고 loss는 CrossEntropy optimizer는 Stochastic Gradient Decent를 사용하였다.
Define train method
def test(epoch):
print(f'\n[ Test epoch: {epoch} ]')
net.eval()
loss = 0
correct = 0
total = 0
for batch_idx, (inputs, targets) in enumerate(testloader):
inputs, targets = inputs.to(device), targets.to(device)
outputs = net(inputs)
loss += criterion(outputs, targets).item()
total += targets.size(0)
_,predicted = outputs.max(1)
correct += predicted.eq(targets).sum().item()
print('\nTest accuarcy:', 100. * correct / total)
print('Test average loss:', loss / total)
if not os.path.isdir('checkpoint'):
os.mkdir('checkpoint')
torch.save(net, './checkpoint/resnet18_cifar10_model.pt')
torch.save(net.state_dict(), './checkpoint/resnet18_cifar10_state_dict.pt')
torch.save({
'model' : net.state_dict(),
'optimizer': optimizer.state_dict()
}, './checkpoint/resnet18_cifar10_all.tar')
print('Model Saved!')- 여기서 torch.save를 통해 모델과 모델의 state_dict 즉 파라미터 값을 한 epoch마다 파일로 저장을 하였다.
Adjust Learning Rate
def adjust_learning_rate(optimizer, epoch):
lr = 0.1
if epoch >= 100:
lr /= 10
if epoch >=150:
lr /= 10
for param_group in optimizer.param_groups:
param_group['lr'] = lr - 위에서 optimizer를 정의할때 lr을 0.1로 하였는데 통상적으로 초기 학습때는 lr을 크게하고 학습이 진행될수록 lr을 낮춰줘야 성능이 좋아진다고 한다. 그래서 현재 epoch 상태를 보고 lr의 크기를 조절하는 함수를 정의했다.
Train and evaluate
for epoch in range(0,20):
adjust_learning_rate(optimizer,epoch)
train(epoch)
test(epoch)
20 epoch을 수행한 결과 정확도가 81.77이 나왔고 학습시간은 약 40분 걸렸다. epoch수를 늘리고 layer가 더 깊었으면 훨씬 더 좋은 결과가 나올 것이다. 이제 학습된 모델을 불러와서 첫번째 batch 즉 32개의 이미지에 대해 얼마나 맞췄는지 확인해보자
Load the model
net = torch.load('./checkpoint/resnet18_cifar10_model.pt')
net.load_state_dict(torch.load('./checkpoint/resnet18_cifar10_state_dict.pt'))
net = net.to(device)- torch.load를 사용하면 쉽게 모델 및 파라미터들을 불러올 수 있다.
Define Visualize method
def imshow(inp, title=None):
"""Imshow for Tensor."""
inp = inp.numpy().transpose((1, 2, 0))
mean = np.array([0.4914, 0.4822, 0.4465])
std = np.array([0.2023, 0.1994, 0.2010])
inp = std * inp + mean
inp = np.clip(inp, 0, 1)
plt.imshow(inp)
if title is not None:
plt.title(title)
plt.pause(0.001) # pause a bit so that plots are updated
def visualize_model(net, num_images=32):
was_training = net.training
net.eval()
images_so_far = 0
with torch.no_grad():
for i, (inputs, targets) in enumerate(testloader):
inputs = inputs.to(device)
targets = targets.to(device)
outputs = net(inputs)
_, preds = torch.max(outputs, 1)
for j in range(targets.size(0)):
images_so_far += 1
fig = plt.figure(figsize=(32,32))
ax = plt.subplot(num_images//2, 3, images_so_far)
ax.axis('off')
ax.set_title('predicted: {}'.format(classes[preds[j]]))
imshow(inputs.cpu().data[j])
if images_so_far == num_images:
net.train(mode=was_training)
return
net.train(mode=was_training)- 32개의 각각의 이미지와 그 위쪽에 모델이 예측한 클래스를 보여주는 함수를 정의하였다.
Visualization
import matplotlib.pyplot as plt
import numpy as np
visualize_model(net, num_images=32)result:
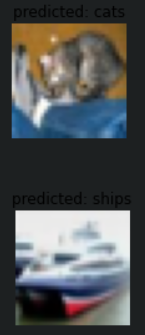
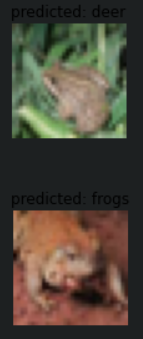

가운데 첫번째 frog를 deer로 예측한것 말고는 대체적으로 잘 맞는 것을 알 수 있다. 직접 세어본 결과 32개중에 4개를 제외하고 다 맞췄다.
이번 포스팅에서는 ResNet에 대해서 알아보았다. 기본적으로 VGGNet과 유사한 구조를 사용했지만, 연산량의 균형을 맞추기 위해 VGGNet과는 다른 모델로 발전을 하게 되었으며, Residual networ 구조를 사용하여 152-layer 라는 아주 깊은 망을 이용해 아주 뛰어는 결과를 얻었고, 이렇게 깊은 망에서도 충분히 학습이 가능하다는 것을 확인 할 수 있었다.
'Deep Learning' 카테고리의 다른 글
| [논문리뷰] MobileNets V1 (0) | 2021.01.04 |
|---|---|
| Batch Normalization (0) | 2021.01.02 |
| [논문리뷰] VGGNet (0) | 2020.12.30 |
| mAP(Mean Average Precision) [1] (1) | 2020.12.16 |
| albumentations (Data Augmentation) (2) | 2020.12.13 |
